Les circuits électroniques digitaux ne peuvent enregistrer que des 0 ou des 1 mais pas de signes + ou -.
Comment donc représenter une valeur négative en mémoire?
Exemple
Dans une voiture le compteur kilométrique s'il ne possède que 6 chiffres ne pourra pas indiquer plus que 999.999 km.
De même, dans les ordinateurs les nombres (binaires) ont aussi des dimensions fixes de 1, 2, 4 ou 8 bytes.
Revenons à l'exemple de la voiture et imaginez un compteur kilométrique qui compte les km en marche avant et qui
les décompte en marche arrière.
Que pourrait-on lire sur un compteur d'une voiture neuve (compteur initialement à 000.000) si elle parcourt 1 km en marche arrière ?
Le compteur décompte 1 km et affiche donc ... 999.999 km !
Ce code correspond parfaitement à la valeur –1 puisqu'on obtient 0 si on lui ajoute à nouveau 1
Dans ce cas 999.999 équivaut à -1.
On exploite cette caractéristique étrange qui est due au fait que ce nombre à une dimension finie ( 6 chiffres décimaux)
De même, quel serait le code d'un nombre de 8 bits pour représenter la valeur –1 ?
Le code 1111 1111(2) = FF(16) convient puisque, si on ajoute 1 à ce nombre, on obtient 100000000(2),
le bit de report déborde à gauche, il sort donc de l'espace qui est réservé au nombre et est donc ignoré!!
Donc nous aurons comme valeur 00000000(2)
Le bit le plus à gauche d'une valeur binaire codée sur un nombre fixe de digits est celui qui va représenter le signe.
Signe négatif si ce bit vaut 1, signe positif quand ce bit vaut 0.
Pour appréhender plus facilement la technique du complément à 2 nous allons illustrer cette technique dans la base 10,
le complément à 10.
Exemple 1:
Imaginons que nous ayons un nombre décimal représenté sur exactement 2 chiffres.
Comment représenter son négatif si nous ne disposons pas d'un signe?
42 - 24 = 42 + (-24) = 18
Si pour la valeur (-24) nous prenons son complément à 10, nous pouvons écrire:
42 + (100 - 24) = 42 + 76 =118
Nous constatons que si nous retirons la valeur du complément, c'est-à-dire 100, nous obtenons 18.
la valeur 76 est donc le complément à 10 de 24, on pourrait l'utiliser comme valeur négative de 24 dans le cas d'une repérésentation décimale sur 2 chiffres.
Exemple 2:
Dans ce cas nous avons un nombre représenté par 3 chiffres, nous voulons pouvoir écrire une représentation de son négatif par un complément à 103.
420 - 209 = 211
Si pour la valeur (-209) nous prenons son complément à 1000 , nous pouvons écrire:
420 + (1000 - 209) = 420 + 791 =1211
Nous constatons que si nous retirons la valeur du complément, c'est-à-dire 1000, nous obtenons 211.
la valeur 791 est donc le complément à 10 de 209, on pourrait l'utiliser comme valeur négative de 209 dans le cas d'une représentation décimale sur 3 chiffres.
Autres exemples:
Représenter la valeur -45 en complément à 10:
100 - 45 = 55
Représenter la valeur -312 en complément à 10:
1000 - 312 = 688
Représenter la valeur -1691 en complément à 10:
10000 - 1691 = 8309
Plus intuitivement on peut constater la chose suivante:
En base 10 les zéros qui précèdent un nombre n'ont aucune influence sur la valeur de ce nombre.
123 ou 00123 ou 00000123 représentent la même valeur.
Dans le complément à 10 je pourrais représenter les négatifs avec un 9 en première position.
En effet, 99999 (pour une représentation sur exactement 5 chiffres représente la valeur -1 car 1 + 99999= (1)00000
La valeur 99999 est bien le complément à 105 de 1.
Donc, si je veux représenter 00024 en négatif, je dois complémenter chaque chiffre à 9 et faire +1
9-0=9, 9-0=9, 9-0=9, 9-2=7, 9-4=5: j'ai donc 99975 auquel j'ajoute 1 : 99976
Vérification: 00042 + 99976 = (1)00018
Une telle écriture fonctionne car le chiffre le plus à gauche (le signe 0 pour le + et 9 pour le −) représente alors simplement l'infinité des chiffres à gauche, cette opération consistant à allonger à volonté l'écriture du nombre à gauche s'appelle l'extension du signe et est bien connue des informaticiens.
Supposons un intervalle de valeurs représenté sur 3 digits décimaux, représentons cet intervalle:

- les valeurs négatives seront représentées par les valeurs 5XX, 6XX, 7XX, 8XX, 9XX
- donc toutes les valeurs dont le premier chiffre est supérieur à 4 sont négatives
- 2 méthodes pour calculer les négatifs:
- 1000 - Nombre
- complément à 9 sur 3 digits + 1
Représentons -24: 1000-24=976 ou (999-24)+1=976
Représentons -389: 1000-389=611 ou (999-389)+1=611
Représentons -500: 1000-500=500 ou (999-500)+1=500
Représentons -499: 1000-499=501 ou (999-499)+1=501
Représentons -2: 1000-2=998 ou (999-2)+1=998
Représentons -726: 1000-726=274 ou (999-726)+1=274
IMPOSSIBLE car le premier chiffre est 2 et ne repésente donc pas une valeur négative.
Représentons 726:
IMPOSSIBLE car le premier chiffre est 7 et il devrait donc être négatif.
Dans une représentation à 3 digits décimaux les valeurs inférieures à 500 et supérieures à 499 ne peuvent pas être représentées!
Pour pouvoir représenter ces valeurs il faut augmenter le nombre de digits.
Quelle est le signe et la valeur (ou magnitude) de 9990 si ce nombre est représenté sur 4 digits décimaux?
- le premier chiffre de 9990 est supérieur à 4 donc le nombre est négatif
- 10000-9990= 10 ou (9999-9990) + 1= 10
La valeur représentée par 9990 est -10
Faisons deux petites additions simples:
- -200 + 100 en complément à 10 sur 3 digits
- -200 + 300 en complément à 10 sur 3 digits
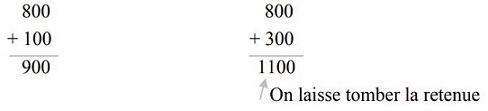
Toute retenue au-delà du nombre de digit n’est
pas prise en compte