Un nombre réel est appelé nombre à virgule flottante car un même nombre peut être représenté en déplaçant la virgule.
Exemple: 1654,234
16542,34 * 10-1
1654,234* 100
165,4234 * 101
etc.
Les nombres sont codés selon un nombre de bits fini, il est donc impossible de représenter la valeur exacte d'un nombre dont la partie décimale est infinie!
Démo
var cpt=1/10,res=0,i=0;
while (i < 10000) {
res+=cpt;
i++;
}
document.write(res.toExponential(20));
On obtient le résultat suivant: 1.00000000000015882051e+3, le résultat contient des décimales parfaitement inattendues!!!
C'est ce genre de surprise qui a mené des missiles Patriote à plusieurs centaines de mètres de leur cible!
On ne peut représenter qu'un nombre fini d'entiers.
Si un nombre est codé sur un byte on ne pourra représenter que des nombre entre -128 (-27) à 127 (27-1)
Si on essaye de faire 120 + 51 par exemple, on ne pourra pas représenter le 171 !!!!
C'est ce genre de surprise qui a mené la fusée Ariane V au fond de l'Atlantique, une valeur de vitesse codée sur 64 bits a été transférée sur une variable codée sur 16 bits: plouf 500 millions à la flotte!
Représentation
Un nombre réel est appelé nombre à virgule flottante car un même nombre peut être représenté en déplaçant la virgule.

Un nombre représenté en virgule flottante est
normalisé en base 10 s’il est sous la forme ± 0,M * 10±e où M est un nombre dont le premier chiffre est non nul.
Exemple:
+ 59,4151 * 10-5 =>
Normalisé: +0,594151 * 10-3
Plage de représentations
- l’exposant est translaté de manière à toujours coder une valeur positive
- pour l'exposant, les valeurs positives possibles sont: [+0, +99]
- En appliquant une translation k=50: les exposants représentables possibles sont [-50,49]
- la constante k est appelée constante d’excentrement

Avec 2 digits pour l'exposant et 5 digits pour la mantisse on peut représenter les valeurs de .00001 x 10-50 à .99999 x 1049
Un nombre représenté en virgule flottante est
normalisé en base 2 s’il est sous la forme ± 1,M * 2±e.
La norme IEEE 754 (Institute of Electrical and Electronics Engineers 754), énoncée par l'ANSI (American National Standards Institute) datée de 1985 dicte la norme de représentation des nombres en virgule flottante.
Cette norme existe en 2 formats:
- Simple précision sur 32 bits
- Double précision sur 64 bits (le JavaScript par exemple)

Représentation sur 32 bits:
- 1 bit de signe
- 8 bits pour l'exposant (e)
- 23 bits pour la mantisse (M)
- Le "1," n'est pas codé, il est implicite
Pour coder les exposants négatifs on décale (k) de 127 (01111111).

Par convention l'exposant 11111111 n'est pas admis, il est utilisé pour définir la valeur NaN (Not a Number).
Pour savoir l'exposant binaire il suffit d'aditionner l'exposant exprimé en b10 et d'ajouter 127, la constante d'excentrement.
Exemple 1
Représentons la valeur numérique réelle -6,625.
- Signe négatif, premier bit à 1
- Valeur absolue en binaire : (6,625)10 = (110,1010)2
- Nous mettons ce nombre sous la forme : 1, partie fractionnaire
110,1010 = 1,101010·22 (22 décale la virgule de 2 chiffres vers la droite)
- La partie fractionnaire étendue sur 23 bits est donc (101 0100 0000 0000 0000 0000)2
- Exposant = 127 + 2 = (129)10 = (1000 0001)2
- Résultat: -(6,625)10 est représenté par (11000000110101000000000000000000)2 en norme IEEE 754
- Résultat en hexadécimal: (C0 D4 00 00)16

Exemple 2
Représentons la valeur numérique réelle -0,625.
- Signe négatif, premier bit à 1
- Valeur absolue en binaire : (0,625)10 = (0,1010)2
- Nous mettons ce nombre sous la forme : 1, partie fractionnaire
0,1010 = 1,010·2-1 (2-1 décale la virgule de 1 chiffre vers la gauche)
- La partie fractionnaire étendue sur 23 bits est donc ( 010 0000 0000 0000 0000 0000)2
- Exposant = 127 + (-1) = (126)10 = (0111 1110)2
- Résultat: -(0,625)10 est représenté par (1 0111 1110 010 0000 0000 0000 0000 0000)2 en norme IEEE 754
- Résultat en hexadécimal: (BF 20 00 00)16

Exemple 3
Représentons la valeur numérique réelle 362,94.
- Signe positif, premier bit à 0
- Valeur absolue en binaire : (362,94)10 = (101101100,1111)2
- Nous mettons ce nombre sous la forme : 1, partie fractionnaire
101101100,1111 = 1,011011001111·28 (28 décale la virgule de 8 chiffre vers la gauche)
- La partie fractionnaire étendue sur 23 bits est donc ( 011 0110 0111 1000 0000 0000)2
- Exposant = 127 + 8 = (135)10 = (1000 0111)2
- Résultat: (362,94)10 est représenté par (0 1000 0111 011 0110 0111 1000 0000 0000)2 en norme IEEE 754
- Résultat en hexadécimal: (43 B6 78 00)16

Valeurs particulières
D'après Wikipédia: le tableau suivant donne la représentation de valeurs particulières.
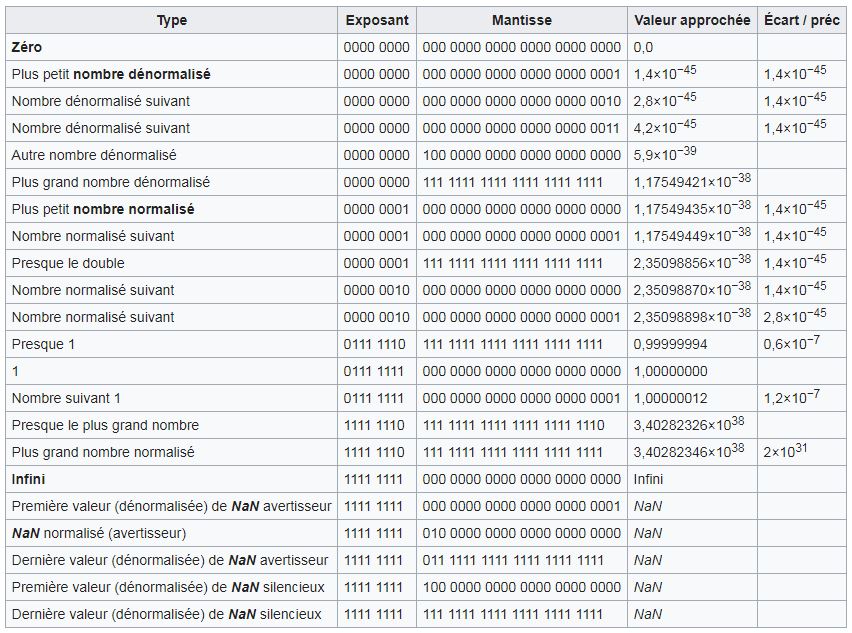

Représentation sur 64 bits:
- 1 bit de signe
- 11 bits pour l'exposant (e)
- 52 bits pour la mantisse (M)
- Le "1," n'est pas codé, il est implicite
Pour coder les exposants négatifs on décale (k) de 1023 (01111111111)
Le mécanisme permettant de représenter une valeur en double précision est exacvtement le même que pour la simple précision